
But this can’t be in general, because it would mean that every map Σ → X \Sigma \to X factors through one of the covering spaces. Now notice how this will in general fail to still be a coequalizer: if it were, for one the morphism ( ∐ i ) → (\coprod_i ) Id ⊣ id ∨ ∨ fermionic ⇉ ⊣ ⇝ bosonic ⊥ ⊥ bosonic ⇝ ⊣ R h rheonomic ∨ ∨ reduced ℜ ⊣ ℑ infinitesimal ⊥ ⊥ infinitesimal ℑ ⊣ & étale ∨ ∨ cohesive ʃ ⊣ ♭ discrete ⊥ ⊥ discrete ♭ ⊣ ♯ continuous ∨ ∨ ∅ ⊣ * Are infinitesimals real Infinitesimals were introduced by Isaac Newton as a means of explaining his procedures in calculus.

If there exists a greatest element of one set or a least element of the other set, then the cut defines a rational number otherwise the cut defines an irrational number.
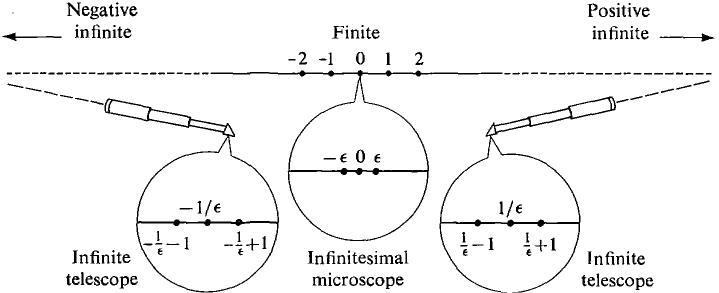
A cut splits the real number line into two sets. Local diffeomorphism, formally étale morphismĮmbedding of smooth manifolds into formal duals of R-algebrasĭerivations of smooth functions are vector fields The status of infinitesimals decreased further as a result of Richard Dedekind’s definition of real numbers as cuts. Pullback of differential forms, invariant differential form, Maurer-Cartan form, horizontal differential form, Vector field, multivector field, tangent Lie algebroid ĭifferential forms, de Rham complex, Dolbeault complex Smooth manifold, smooth structure, exotic smooth structureįormal smooth manifold, derived smooth manifold Infinitesimal space, infinitesimally thickened point, amazing right adjointĭifferentiable manifold, coordinate chart, atlas The simplest way to add an infinitesimal to an ordered ring (or rig) is freely.
Are infinitesimals real how to#
So the interesting question is how to get other infinitesimals.

Geometry of physics: coordinate systems, smooth spaces, manifolds, smooth homotopy types, supergeometry In the usual systems of numbers (real, natural, complex, cardinal, etc), 0 0 is the only infinitesimal number. From point-set topology to differentiable manifolds The set of reals is infinite and not countable: there does not exist a method of making finite representations or codings of real numbers.


 0 kommentar(er)
0 kommentar(er)
